フェルミ推定や、仮説思考などが、今ビジネスでも、大流行ですね。
書店にいっても、そういった類の本が、いっぱい並んでいます。
色んな情報にあふれている今、単なる過去の統計やデータだけでは、判断材料と出来ず、そういった推定をしていく能力が、求められているんでしょうね。

そんな中でも、ベイズ推定 今、ちょっと確率の世界では話題です。
今回は、ベイズ推定にについて、例題と共に、お伝えしたいと思います。
ベイズの定理
まず、ベイズの定理について見て見ましょう。
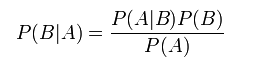
- P(A) : A が起きる確率
- P(B) : B が起きる確率(事前確率と呼ぶ)
- P(A|B) : B が起きた後で、A が起きる確率(条件付き確率、尤度と呼ぶ)
- P(B|A) : A が起きた後で、B が起きる確率(条件付き確率、事後確率と呼ぶ)
なんだか、これでは意味がさっぱりわかりませんよね?(笑)
こういう公式だとか定理は、例題を解いて試してみないと、大概よくわかりません。
例題を解いてみましょう。
ベイズ推定で、必ず出てくるのがこの問題です。
「モンティ・ホール問題」
これは、アメリカのクイズ番組で実際にあったようです。
モンティ・ホールというのは、そのクイズ番組の司会者の名前です。
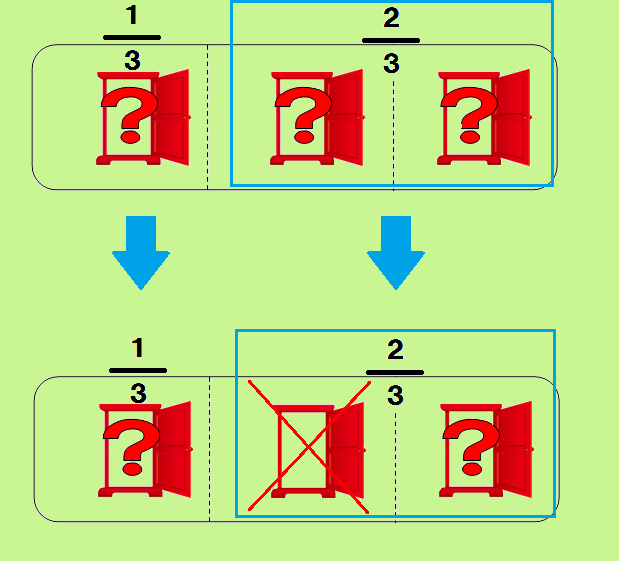
ここに、3つのドアがあります。
どれか1つには、ドアの向こうに豪華賞品があり、それ以外はハズレ(空)です。
どのドアの裏に豪華賞品があるかは、司会者のモンティは知っています。
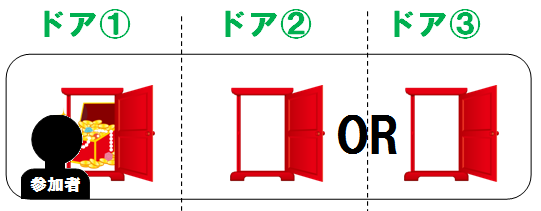
参加者は、まず、3つのうち、どれか1つを選び、司会者のモンティに伝えます。
モンティは、それを受けて、残りの2つのドアから1つ、空のドアを開けます。
そして、あらためて参加者に、どちらかを選ぶように伝えます。
今、参加者が、ドア①を指定しました。
モンティは、残りのドア② と ドア③ から、ドア②を開けました。
参加者は、ドア① か ドア③ をあらためて選ぶことになります。
どちらが確率的に有利でしょうか?
この問題、一見、ドア① か ドア③ の2択なので、確率1/2で、同じなんじゃないの??って思ってしまいます。
ところが、違うんです。
いきなり、ベイズの定理の公式に当てはめるのではなく、解いてみましょう。
モンティホール問題の解
まず、最初に、ドア①を選んだ時に、豪華賞品に当たる確率はどうか?
これは、簡単ですね。
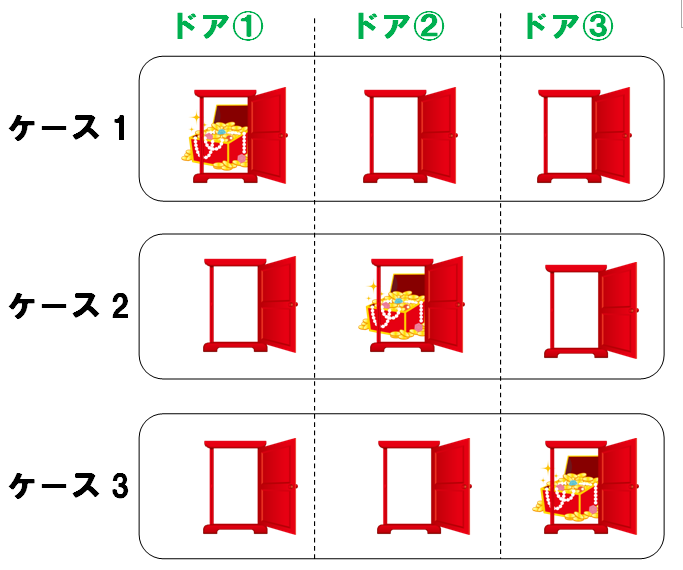
この通り、3つあるケースの内の1つなので、確率1/3です。
ドア②でも、③であっても、同じで確率1/3です。
さて、問題はここでモンティが空のドア②を、開けることです。
こ の確率1/3が、一体どの様に変化するのか?
まずドア① に豪華賞品 があったと仮定します。
【仮定1】 ドア① に豪華賞品がある場合
モンティは、ドア② と ドア③ のどちらも開けることができます。
つまり、ドア② を開ける確率は 1/2 です。
従って、ドア① に豪華賞品があって、ドア②を開ける確率は・・・
1/2 × 1/3 = 1/6 です。
続いて、ドア③ に豪華賞品があったと仮定します。
(仮定2)ドア③ に豪華賞品がある 場合
モンティは、ドア② しか開けることができません。
つまり、ドア② を開ける確率は100%で1/1 です。
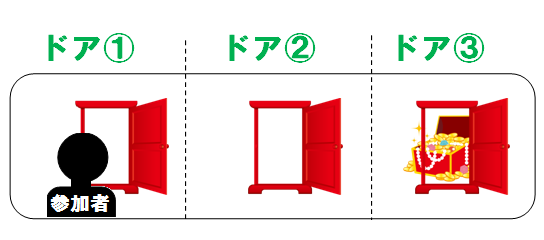
従って、ドア③ に豪華賞品があって、ドア②を開ける確率は・・・
1/1 × 1/3 = 1/3 です。
確率に、「2倍」もの差があるということです。
つまり、参加者は、選択を変えた方が、2倍も賞品が当たる確率が増えるんですね。
さて、では次に、ベイズの定理を使って解いていきましょう。
そして、実際の「条件付の確率」を出します。
ベイズの定理での解
モンティによってドア②が開放されて、空だということが判明した後に、
ドア①を選ぶか、ドア③を選ぶかです。
求める確率は、次の2点になります。
- ドア②が開いた後に、ドア①に豪華賞品がある確率
- ドア②が開いた後に、ドア③に豪華賞品がある確率
では、まず仮定1のケースから見ていきます。
ドア①の場合
P(B|A) : ドア②が開いた後に、ドア①に豪華賞品がある確率
P(A) : ドア②が開く確率
P(B) : ドア①に豪華賞品がある確率 (事前確率)
P(A|B) : ドア①に豪華賞品があった場合に、ドア②を開く確率(条件確率)
P(A) は、以下の様に求められます。
ドア②に豪華賞品があった場合には、開けられませんので0です。
ドア③に豪華賞品があった場合には、1/3です。
これらを足したものがP(A)ですので、 P(A) = 1/6 + 1/3 + 0 = 1/2
P(B)は、3つあるケースの内の1つですから、1/3 です。
P(A|B)は、これは、先ほど計算した、1/2 です。
これらを計算します。
P(B|A) = P(A|B) × P(B) / P(A) P(B|A)
= (1/2) × (1/3) / (1/2)
= 1/3
次に、仮定2 のケースです。
ドア③の場合
P(B|A) : ドア②が開いた後に、ドア③に豪華賞品がある確率 (条件確率)
P(A) : ドア②が開く確率
P(B) : ドア③に豪華賞品がある確率(事前確率)
P(A|B) : ドア③に豪華賞品があった場合に、ドア②を開く確率
P(A)は先ほどと同じ1/2
P(B)も、同じ1/3
P(A|B)は、1/1 (100%)
これらを計算します。
P(B|A) = P(A|B) × P(B) / P(A) P(B|A)
= (1/1) × (1/3) / (1/2)
= 2/3
結果
条件確率がそれぞれ求められました。
ドア① に豪華賞品がある確率は、1/3
ドア③ に豪華賞品がある確率は、2/3
その他の解法
ベイズ推定なので、あえてベイズの定理で計算しましたが、この問題実はもっと簡単に解けます(笑)
それが、次の方法です。
豪華賞品のある確率は、各ドアとも1/3 ずつです。
つまり、参加者が選んだ以外のドアは、2/3でした。
その内の、一つが無くなったので、選んだドアが1/3、そうでないほうが2/3です。
直感的に、分かりづらいかもしれませんね(笑)
その場合には、ドアの数を増やせば、納得がいきます。
ドアが1000個あった場合に、選んだドア以外から、モンティが、998個の空のドアを開けたとします。
残った2つのうち、どっちに豪華賞品がある確率が高いかは、直感的に分かりますよね。
あとがき

確率は、本当面白いですよね。
数学の中でも、結構実用的なものだと思います。
確率の本って、本格的なものだと集合の記号とかで、全然身近じゃないんですよね・・・
ましてや、ベイズ確率となると、ベイズ統計やベイズフィルターなど、本格的に、それで仕事をする人や大学で学ぶ人の本しかないですよね。
これって、一般の確率(頻度確率)と同じように、普段の生活で使えると思うんですよね。 受験や、コンピューターといったものでなく、もっと身近なものを扱った本が増えたらなぁ~と思うんですけどね。
また、こういった話題は、ちょこちょことお届けしたいと思います。
ちなみに、ベイズ定理は確率の基本から簡単に導き出せます。
別の投稿で出していますので、よければそちらも、ご覧下さい。
⇒ ベイズの定理の証明!?意外と簡単な確率の計算でした!




コメント
ドア①の場合において、
P(B|A) = P(A|B) × P(B) / P(A) P(B|A)
とありますが、分母が誤っています。これをP(A)のみとするもしくは全確率の定理に基づいて展開するのが正しいベイズ理論の適用です。
モンティホール問題は、条件付き確率を求めるものではありません。例えると「トランプ問題」で最初にダイヤを選ぶ確率(1/4)を求めるもので、3枚のダイヤが出たときに限定して条件付き確率(10/49)を求めるものではありません。モンティホール問題で、モンティが必ずハズレのドアを開けるなら、事前確率(最初に選択したドアが当たる確率)は変化しません。
モンティホール問題は、モンティ司会の番組でこの中で3つの扉で、回答者が選んだドア以外の内、空の扉を開けるというものです。
以外の数学のサイトを参考にしています。
http://mathworld.wolfram.com/MontyHallProblem.html
モンティホール問題は、条件付き確率を求めるものではないので、ベイズの定理は必要ありません。この問題を、条件付き確率の問題と考えると、解答は得られません。
[…] 会者がBを開けて、何もない。その後に、AかBどちらかを選びなおせるときに、選びなおすかどうか?という問題。これは、Bに選びなおした方が確率が1/3から2/3に上がる。解説はコチラ。 […]