ベイズ推定・統計の基本となる、ベイズの定理。
この定理、なんだかなじめないという人が、意外と多いんですよね。
Thomas Byayes 1702-1761
ベイズ推定・統計を使いこなす「ベイジアン」になるには、まず、このベイズ確率の基本となる、ベイズの定理を覚えなくてはいけません。
この定理の証明は、とても簡単です。
また、意味が分かれば、簡単に覚えてしまいます。
ここでは、そんなベイズの定理の証明を、誰でも分かるように、確率の基礎から丁寧に、解説をしていきます。
勉強ではなく、ゲームの解説でも聞くような気楽な気持ちで、楽しんで見て下さい（笑）
ベイズの定理
さて、まず最初にベイズの定理について、見てみましょう。
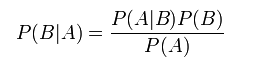
- P(A) : A が起きる確率
- P(B) : B が起きる確率（事前確率）
- P(A|B) : B の後でA が起きる確率（条件付き確率、尤度）
- P(B|A) : A の後でB が起きる確率（条件付き確率、事後確率）
さて、それではこれを簡単に解説をしていきます。
まずは、ベイズの定理の理解に必要な確率の基本を、簡単におさらいしましょう。
確率の基本
ベイズの定理は、覚え難そうに見えますが、確率の基本の乗法定理を組み合わせただけです。
まずは、乗法定理をしっかりと押さえておきましょう。
乗法定理（積の法則）
乗法定理を使う確率の問題は次の様なものがあります。
さて、この問題を見て分かるとおり、確率1/6 と 1/2のかけ算（乗法・積算）することで、確率が求められています。
でも、なぜ掛け算なんでしょうか？
これは、次の図を見れば分かります。
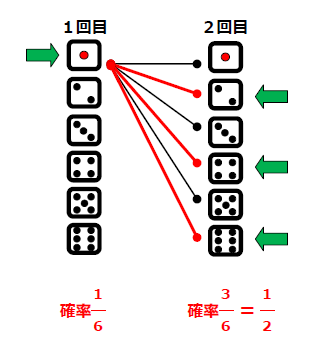
1回目で、確率1/6のものが、更に2回目で、その確率が半分（1/2）になるので、確率は1/12になります。
ここで、大事な事は、１回目に１、２回目に偶数という、二つの事象が同時に成り立つ確率は、それぞれの確率を掛け合わせればよいということです。
これを、「同時確率」といいいますが、確率の乗法定理は、この同時確率を、求めるための公式です。
さて、それでは次の問題を見てみましょう。
条件付確率：同時確率との関係
１ヶ月間の売上げを見たところ、次の様な結果が出た。
| １ヶ月間の、お客様全員の数 | ３００名 |
| アマイーを注文したお客様の数 | ４０名 |
| ニガイコーヒーを注文したお客様の数 | １００名 |
| ニガイコーヒーを注文して、アマイーを注文したお客様の数 | ２０名 |
これを、ベン図で書くと、この様になります。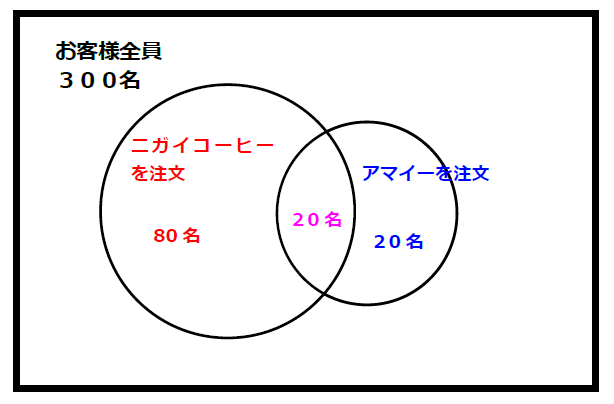 
さて、このデータをもとに、次に来たお客様について考えてみましょう。
ニガイコーヒーとアマイーの両方を注文する確率は、一体、どれくらいでしょうか？
これは、さっきのサイコロと同じで、同時確率を求めれば、いいですよね。
- ニガイコーヒーを注文する
- アマイーを注文する
この２つの事象が同時に成り立つ時の確率です。
答えは、簡単ですね。
全体の300のうち、両方を注文したお客様は20名なので、BとAの同時確率は、20/300 = 1/15 です。
さて、ここからが、おもしろくなります（笑）
B と A の同時確率
この同時確率は、次の2つを使って表現することができます。
- 全体の中で、ニガイコーヒーを注文したお客様の確率
- ニガイコーヒーを注文したお客様で、アマイーを注文したお客様の確率
- まず、１番からです。
お客様全員は300名で、その内、ニガイーコーヒーを注文したお客様は100名です。
従って、確率は
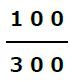
- 続いて、２番です。
ニガイコーヒーを注文したお客様が100名、その中でアマイーも注文したお客様は20名です。
従って、確率は
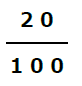
この1番と2番を使って、同時確率（ニガイコーヒーとアマイーの両方を注文する確率）を求めると・・・
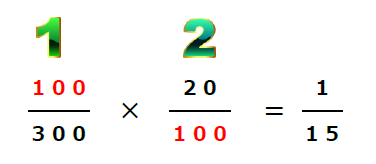
この100は、ニガイコーヒーを注文したお客様の数です。
一般化する為に、次の様に置き換えます 。
- アマイー を注文 ⇒ 事象A
- ニガイーコーヒーを注文 ⇒ 事象 B
ニガイコーヒーを注文する確率
B が起こる確立
P（B）
ニガイコーヒーを注文したという条件で、アマイーを注文する確率
B が起きた後で A が起きる確率（条件付き確率）
P(A|B)
同時確率は、これらを、掛け算すればよいので、次の様になります。
ここで、先ほどの、ベイズの定理を、もう一度見てみてください。
この同時確率の式が、そのままベイズの定理の「分子」の部分であることが分かると思います。
さて、それでは、いよいよベイズの定理の証明にいきましょう。
ベイズの定理の証明
証明には、B と A の同時確率は、A と B の同時確率 から導きますが、これらは共に答えは同じです。
念の為、さっきの、ニガイコーヒー（B）と、アマイー（A）の例で見てみましょう。
A と B の同時確率
- 全体の中で、アマイーを注文したお客様の確率
- アマイーを注文したお客様で、ニガイコーヒーを注文したお客様の確率
- まず、１番からです。
お客様全員は、300名で、その内、アマイーを注文したお客様は40名です。
従って、確率は
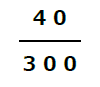
- 続いて、２番です。
アマイーを注文したお客様は40名で、その中でニガイコーヒーを注文したお客様は20名です。
従って、確率は
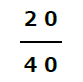
この1番と、2番を使って、同時確率（ニガイコーヒーとアマイーの両方を注文する確率）を求めると・・・ もう、お分かりですよね。
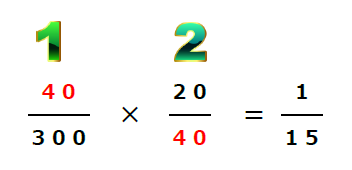
この値は、さっきのB と A の同時確率の答えと同じですよね。
証明最終段階
さて、BとAの同時確率 ＝ AとBの同時確率 という事がはっきりとしました。
改めて、この２つの、同時確率の条件付き確率から求める式を見てみましょう。
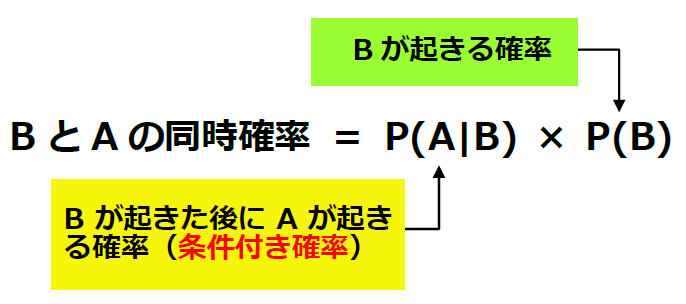
- BとAの同時確率 ＝ B の後でAが起きる確率 × Bが起きる確率
- AとBの同時確率 ＝ A の後でB が起きる確率 × Aが起きる確率
左辺同士がイコールなので、右辺同士もイコールですよね。
これを、次の様に一般式で書きます。
- P(A) : A が起きる確率
- P(B) : B が起きる確率（事前確率と呼ぶ）
- P(A|B) : B の後でAが起きる確率（条件付き確率・尤度と呼ぶ）
- P(B|A) : A の後でB が起きる確率（条件付き確率・事後確率と呼ぶ）
お疲れ様でした、ベイズの定理の完成です！
ベイズの定理といっても、確率の乗法定理を組み合わせて、変形させただけなんです。
乗法定理の、同時確率が条件付き確率をかけて求めるというところが、分かっていれば、何ということはないですよね。
まとめ
ベイズの定理の証明同時確率と条件付き確率
BとAの同時確率 ＝
B の後で A が起きる確率（条件付き確率） × Bが起きる確率
BとAの同時確率 ＝ AとBの同時確率
つまり・・・
B の後で A が起きる確率（条件付き確率） × Bが起きる確率は、
A の後で B が起きる確率（条件付き確率）× Aが起きる確率と同じ。
これを一般式にして、両辺をP(A)で割る
あとがき
ベイズ確率って、最近のトレンドの様に使われているので、少なくとも20世紀後半に誕生したのかと思っていました。
このベイズさんって、1702年生まれなんで驚きました。
実際に、ベイズ確率が広まったのは、その後、ラプラスによって18世紀後半から19世紀にかけてのようですね。
時代が、こう目まぐるしく変化し、次から次へと新製品が出てきたり、新しいシステムが出来たりすると、故障率や、何か経営戦略的な数値を出すのも、従来の頻度に頼る確率・統計では対応できないですよね。
このベイズの定理を元とした、ベイズ推定やベイズ統計などが、本当に今はメジャーですよね。
ベイズの定理については、他にも投稿があるので、よろしければそちらもご覧下さい。
⇒ベイズ推定！例題でモンティ・ホール問題を解いてみた
コメント