「 対数 」 どんなイメージがありますか？
指数は、まだ使うけど、対数って高校で習ったきり・・・という方が多いかもしれません。
大学や専門学校でも理数系や経済でないと、あまり使わないですよね。
「対数」というと、高校時代「公式」を覚えさせられて、何に必要なのかも分からず、試験問題の計算ばかりをやらせれていた・・・そんな感じですよね（笑）
とっつきにくい印象があります。
でも、対数って、意外にも、とても身近に使われているものもあります。
その代表が、地震の「マグニチュード」 です。
地震のエネルギーを、対数を使って表しています。
今回は、そんな対数について、公式や計算はもちろんですが、対数の意味についても、できるだけ、分かりやすく説明をしたいと思います。
指数と対数の関係
対数は分からなくても、指数は分かるという方は多いですよね。 例えば、102（10の2乗）は、100ですよね。 実は、対数は、この指数の表し方を逆にしたものです。
具体的に、今の指数を例にとります。
この式の意味は、 「10を2乗すると？ 答えは 100」
これを、対数で表現すると・・・
この式の意味は、「 10を100にするには何乗？答えは2」
これを、一般式で書くと次のようになります。
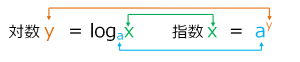a : 底（てい） ｘ： 真数
何乗しているのか？を求めているのが、対数なんですね。
慣れるために、実際にいくつか、計算してみましょう。
練習問題
計算そのものは、「何乗しているか」を求めているだけです。
「何乗しているのか」を求める事に、何の意味があるのでしょう？
計算が出来るだけでなく、対数そのものの意味を、きちんと理解しておきたいですよね。
対数の意味
対数は、指数とセットで考えた方が、簡単に理解ができます。
指数は、とても便利ですよね。
例えば、100,000,000,000 なんていう数値を・・・
「1011 」
10の11乗、たったこれだけで、表現できてしまいます。
この11というは、そのまま”桁”を表していますよね。
対数は、実は「桁」を求めていたんです。
例えば、10 と 1,000,000 という数字は、対数なら 1 と 6 で表現できてしまいます。
数値を扱う場合に、手頃な数字の置き換えられるので、対数はとても便利なんです。
1000000000000000000000000000000 なんていう数字を、そのまま使っていたら面倒ですよね（笑）
この様に、10を底とした対数は、普段使われる10進数では、桁を変えることになります。
2進数や、8進数などはコンピューター関係でなければ、あまり使うことは無いと思います。
10進数だけは、特別で「常用対数」（じょうようたいすう）と呼ばれています。
高校の時、常用対数表って使いましたよね
log102 や log103などは、暗記させられた人もいるかもしれません（笑）
対数表が無くても、関数電卓があれば簡単に計算することが出来ます。
では、この常用対数、実際にどんなケースで使われるかというと、天文学や、それから冒頭にも述べた、地震のマグニチュードです。
こういったものは、大きな数値を取り扱うので、対数が無いと面倒なんですね。
さて、対数の意味が分かったところで、次に、対数の公式を見ていきましょう。
対数の公式
対数の公式ですが、次の公式があります。
実際に例題を、解きながら覚えてしまいましょう。
練習問題
どうでしたか？
分かってしまえば、簡単なことですよね！
それでは、最後に簡単に、まとめます。
まとめ
対数 対数の意味
- 底（a）を10の場合、これを常用対数と呼ぶ。
- 10進数を扱っている場合には、対数は「桁」を意味する事となり。
大きな値を使うのに便利
例） 天文、地震(マグニチュード）など
対数と指数の関係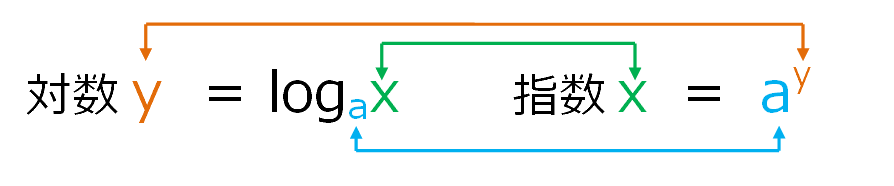 
対数の公式
あとがき
「対数」高校時代は、あまり何とも思っていなかったんですけど、結構便利なんですよね。
計算そのものは、ExcelやProgramにさせるので、あまり手計算することの方が少ないかもしれません、計算するにしても関数電卓ですしね・・・（笑）
数学は、やはり「意味」がとても大事ですよね。
対数にしても、指数、それから三角関数などにしても、それが必要となる理由があって生まれています。
なぜそれが必要なのかがわかると、興味もわきます。
そして、数学の知識が無いと、読んでもチンプンカンプンっていう本は、結構ありますしね。
どうせ勉強するのなら、生きた知識を身につけたいですよね。
コメント
loga-logb=loga/bは理解できます。では-logb/aが成り立つのか教えてください。宜しくおねがいします。
-(loga-logb)=-loga/bは成りたちますが…
-logb/a=log(b/a)^(-1)=loga/b
成り立つんじゃね？
常用対数の説明大変よく分かりました。
最後に少しだけ自然対数のさわりを書いていただけら学習が進展していくのでは無いかと思います。
コメントありがとうございます。
たしかに、その通りですよね。
ご指摘ありがとうございます、検討いたします。
計算尺では常用対数をメモリにして、二個の物差しを作り、それをスライドさせて、足し算、引き算をしますが、これが掛け算、割り算になることを考えたのですね。
自然数の物差しを二つ利用して、足し算、引き算出来ることはそれより前に知っていた。
何回読んでもわからねーや。
書いてもわからねーや。
敷居が高すぎるか説明が下手のどっちかだね。
オタク同士の会話みたいで理解できん。
数学脳の連中は国語がまずメタメタにだめだなんだよな。
やり直し。
kenkenさんではないので関係ない奴が首突っ込むなと言われればそれまでですが…
私はまだ授業で対数を扱っていません。ですがこのサイトを見れば全て理解できました。（自慢ではないです。）
kenkenさんは理解しやすいように親切にも練習問題、その解説まで書いてくれています。こんなことをいうのは大変失礼なのですが、おそらくあなたの理解力が足りないだけかと。
ついさっき対数を理解したばかりのやつにこんなことを言われるのは癪に障るかもしれませんが、あえて言わせていただきます。
きちんと最初から完璧に理解するようにしていますか？
基礎が固まっていないのに先に進んだところで理解できないのは当たり前です。
もし少しでも理解できていないところがあるのなら、そこをつぶしていくことが最優先事項です。
それから、練習問題をきちんと解くことも内容を定着させるうえで非常に大事なことです。解説を読んだところで自分の力のみで解けるようにならなければなんの意味も持ちません。わからなければ教師だとか、このようなサイトの主に尋ねればいいのです。あなたのように他人を否定していては成長することはできないといっても過言ではないです。「オタク同士の会話みたい。」とおっしゃってますが、それはつまり書いてあることが難しくて理解できない、ということですかね？
もしそうなのであれば、まずは理解しようとしてください。まあ「何回読んでもわからない。」とのことなので努力しようとはしているはずです。しかし、考えてもわからないから「もういーや。」といって途中であきらめてしまっているのでは？それなら非常にもったいないです。人間は一度完璧に理解すると1週間程度あいても大丈夫、むしろ1週間後、2週間後という周期で復習をしたほうが定着しやすい、といったことが科学的に証明されています。そのため、最初はどんなに時間をかけてもいいのでまず一度完璧に理解してみてください。何日かけてもかまいません。たとえ3日、5日かかったとしても完全理解してしまえば勝ちなのですから。
お前ごときに言われたところで説得力ねーよ、と思われるでしょうが、これはすべて私の担任の受け売りです。生徒のために勉強のためになることを毎日毎日調べてくれるような先生です。やはりその気合が空回りしてウザがられたりもしていますが、なかなか他人のためにそこまでできる人もいないと思います。私は恵まれていると思います。
少々話が脱線してしまいましたが、とにかく一度理解してみてください。これは何も対数だけではない、すべての範囲、すべての教科においていえることなのですから。もし一回だけやってみるか、となった時復習を怠ることは忘れないでください。一週間に一度を二週間続けた（二回復習した）あとは1ヶ月だったり、復習ペースを自由に変えればよいです。一度だけ私のことを信じてみてください。
長々と書いてしまいすみませんでした。応援しています。
数学脳って論理的思考力だよ。
一般的に数学ができる人の文章のほうが、
数学ができない人の文章よりわかりやすい。
数学ができる人の国語(国語？現代文か？)がメタメタってのは
一般的じゃないよ。むしろ逆なくらいだな。
あなたが理解できないのを、他人のせいとして”責任転嫁”する行為はよくないと思います、そのような風に「俺はわるくねぇ、悪いのはお前だ」という思考をしているから理解が一切できないのだと思います。
そもそもの問題としてあなたの書いてるコメントの文章も箇条書きで、言いたいことが伝わりにくくなっています、こういう時は単刀直入に、「俺わかんねぇや、まるでオタク同士の会話みたいだね、数学得意な連中は国語ができないからダメなんだよね、書き直して」と書き込めば良いのです。
理解できましたか？。
すいません、2logxなどlogの前に数字が付いている場合などはどうすればいいのでしょうか？
ZIPneaさん、コメントありがとうございます。
2logxは、「2 x logx」の事です。
上記、公式3の n も同じことです。
[…] 対数の解説 […]
私は今数三をしているのですが、logの範囲が全くわかりません。
で、質問なんですが、logの中にlogが出てくることはあるのでしょうか。
Logの中にLogが使われることももちろんあります。指数の中に指数が使われるのと同じです。
∫（１／ｘｌｏｇｘ）ｄｘとか
まさにそうなるかと思います
仕事でｄBの計算をする必要があり、ここを参考にさせて頂きました。
大変分かりやすく、理解するまでの時間が短縮出来たと思います。
ありがとうございました。